101.1 Introduction to wrstcse

wrstcse provides a few approaches to worst case calculations that are powerful enough for most engineering problems, but avoid the problems that make a true interval arithmetic unfeasible for non-trivial problems:

• Extreme worst case calculation by determining which combination of extreme input values will yield the most extreme result (wc_mintypmax, wc_systematic). Its approach isn’t guaranteed to find local minima and maxima in the middle of the input parameter space. In most real-world problems, though, the derivation of the result to each parameter doesn’t change its sign in the tolerance space, which moves the extreme cases to the edges of the tolerance space making them accessible to this method. Via wc_ewc_simplify this method can typically be reduced from a brute-force approach to being O(n)-complete.
• The monte carlo approach that assigns each parameter random values in the tolerance space and, when repeated n times will yield a view of the distribution n samples might have. The view provided by this method is pessimistic, as most real-wprld items are more probabible to lie in the middle of the tolerance space than at its end.
• The root mean square approach that knowing an approximation of the parameters of the gaussian distribution of the input values one can determine how big the tolerances will realistically be if one requires a given yield (see wc_mintypmax_rss). Note that even rectangles tend to quickly add up to approximation of gauss curve, if affecting the same tolerance which makes this method applicable to most real-world problems.

Tolerances are applied to parameters by providing each tolerance-laden parameter with a tol[n] that wrstcase will vary between -1 and 1 looking for extreme results, while rol[n]=0 should yield the typical value of a parameter.. Using the same n for two parameters will make both parameters have coupled tolerances. Therefore two 1% resistors that both will change over the temperature range by another 2% in the same way can be defined as follows:

(%i1) load("wrstcse")$

(%i2) vals: [
   R_1= 1000.0*(1+tol[1]*.01)*(1+tol[3]*.02),
   R_2= 2000.0*(1+tol[2]*.01)*(1+tol[3]*.02)
 ];
(%o2) [R_1 = 1000.0 (0.01 tol  + 1) (0.02 tol  + 1), 
                             1               3
                    R_2 = 2000.0 (0.01 tol  + 1) (0.02 tol  + 1)]
                                          2               3

(%i3) R_1+R_2=wc_mintypmax(subst(vals,R_1+R_2));
(%o3) R_2 + R_1 = [min = 2910.6, typ = 3000.0, 
                                        max = 3090.6000000000004]

(%i4) R_1+R_2=wc_mintypmax_percent(subst(vals,R_1+R_2));
(%o4) R_2 + R_1 = [min = - 2.980000000000005 %, typ = 3000.0, 
                                      max = 3.0200000000000227 %]

(%i5) R_1/R_2=wc_mintypmax(subst(vals,R_1/R_2));
      R_1
(%o5) --- = [min = 0.4900990099009901, typ = 0.5, 
      R_2
                                        max = 0.5101010101010102]

(%i6) R_1/R_2=wc_mintypmax_percent(subst(vals,R_1/R_2));
      R_1
(%o6) --- = [min = - 1.980198019801982 %, typ = 0.5, 
      R_2
                                       max = 2.020202020202033 %]

load ("wrstcse") loads this package.

101.2 Functions and Variables for wrstcse

Function: wc_typicalvalues (expression) ¶

Returns what happens if all tol[n] happen to be 0, which moves all parameter to the middle of their tolerance range.

Example:

(%i1) load("wrstcse")$

(%i2) vals: [
   R_1= 1000.0*(1+tol[1]*.01),
   R_2= 2000.0*(1+tol[2]*.01)
 ];
(%o2) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_2 = 2000.0 (0.01 tol  + 1)]
                                                          2

(%i3) divider:U_Out=U_In*R_1/(R_1+R_2);
                                R_1 U_In
(%o3)                   U_Out = ---------
                                R_2 + R_1

(%i4) wc_typicalvalues(vals);
(%o4)             [R_1 = 1000.0, R_2 = 2000.0]

(%i5) wc_typicalvalues(subst(vals,divider));
(%o5)            U_Out = 0.3333333333333333 U_In

Function: wc_inputvalueranges (expression, [show_tols]) ¶

Convenience function: Displays a list which parameter can vary between which values.

If show_tols is true then this function additionally displays which tol[n] each variable is affected by.

See also wc_mintypmax2tol and wc_inputvalueassumptions.

Example:

(%i1) load("wrstcse")$

(%i2) vals: [
   R_1= 1000.0*(1+tol["R_1"]*.01+tol["Temp"]*.001),
   R_2= 2000.0*(1+tol["R_2"]*.01+tol["Temp"]*.001),
   R_3= 2000.0*(1+tol["R_3"]*.01)
 ];
(%o2) [R_1 = 1000.0 (0.001 tol     + 0.01 tol    + 1), 
                              Temp           R_1
R_2 = 2000.0 (0.001 tol     + 0.01 tol    + 1), 
                       Temp           R_2
R_3 = 2000.0 (0.01 tol    + 1)]
                      R_3

(%i3) wc_inputvalueranges(vals);
(%o3) 
    [ R_1  min = 989.0   typ = 1000.0  max = 1010.9999999999999 ]
    [                                                           ]
    [ R_2  min = 1978.0  typ = 2000.0  max = 2021.9999999999998 ]
    [                                                           ]
    [ R_3  min = 1980.0  typ = 2000.0        max = 2020.0       ]

(%i4) wc_inputvalueranges(vals,true);
               [ R_1 ]         [ min = 989.0  ]
               [     ]         [              ]
(%o4)  Col 1 = [ R_2 ] Col 2 = [ min = 1978.0 ]
               [     ]         [              ]
               [ R_3 ]         [ min = 1980.0 ]
         [ typ = 1000.0 ]         [ max = 1010.9999999999999 ]
         [              ]         [                          ]
 Col 3 = [ typ = 2000.0 ] Col 4 = [ max = 2021.9999999999998 ]
         [              ]         [                          ]
         [ typ = 2000.0 ]         [       max = 2020.0       ]
         [ [tol    , tol   ] ]
         [     Temp     R_1  ]
         [                   ]
 Col 5 = [ [tol    , tol   ] ]
         [     Temp     R_2  ]
         [                   ]
         [     [tol   ]      ]
         [         R_3       ]

Function: wc_systematic (expression, [num]) ¶

Systematically introduces num values per parameter into expression and returns a list of the result. If no num is given, num defaults to wc_defaultvaluespertol. Negative values for num make wc_systematic use the monte carlo method with num samples, instead.

If an equation uses the following values with tolerances:

vals:[R_1=100+tol[1],R_2=100+tol[2]];

num=2 will cause the following combinations of tolerances to be tested: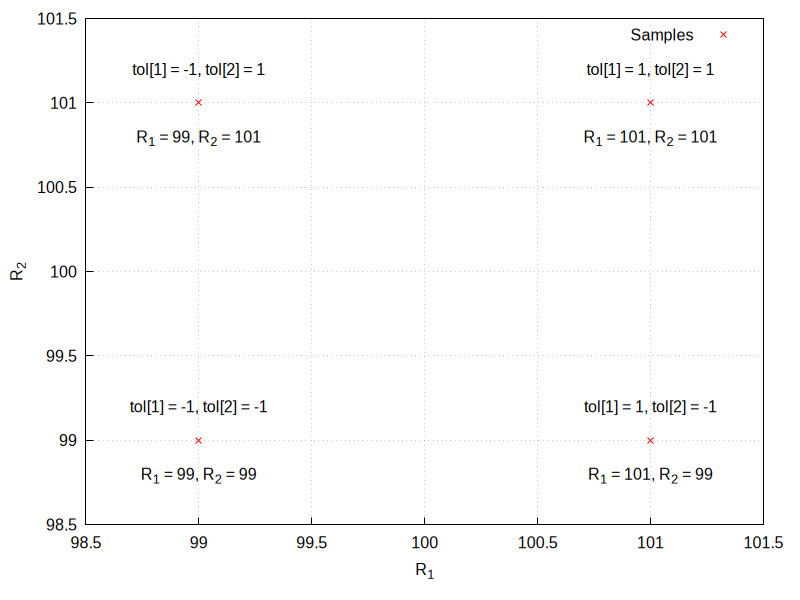 num=3 will cause the following combinations of tolerances to be tested: num=-500 will cause the following combinations of tolerances to be tested, instead: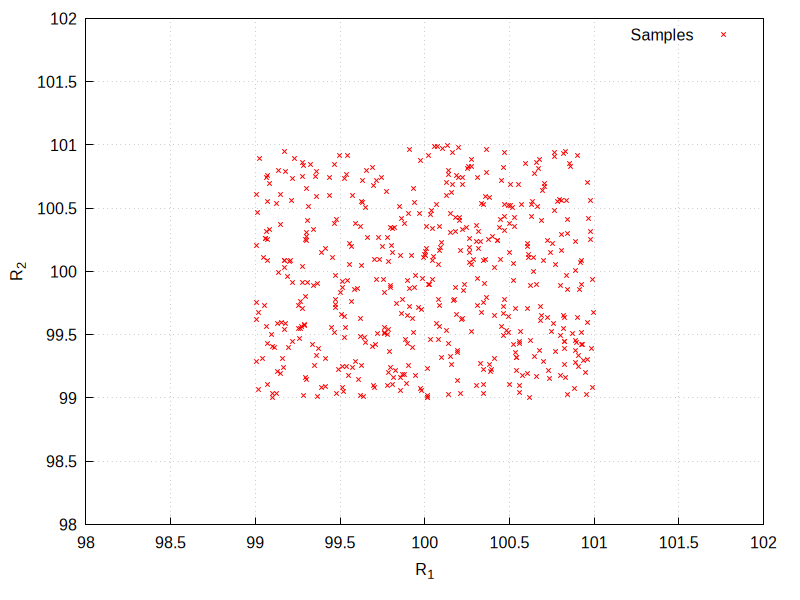

See also wc_defaultvaluespertol, wc_mintypmax, wc_defaultvaluespertol, wc_ewc_simplify and wc_montecarlo.

Example:

(%i1) load("wrstcse")$

(%i2) vals: [
   R_1= 1000.0*(1+tol[1]*.01),
   R_2= 2000.0*(1+tol[2]*.01)
 ];
(%o2) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_2 = 2000.0 (0.01 tol  + 1)]
                                                          2

(%i3) divider: U_Out=U_In*(R_1)/(R_1+R_2);
                                R_1 U_In
(%o3)                   U_Out = ---------
                                R_2 + R_1

(%i4) wc_systematic(subst(vals,rhs(divider)));
(%o4) [0.33333333333333337 U_In, 0.3311036789297659 U_In, 
0.3289036544850498 U_In, 0.3355704697986577 U_In, 
0.3333333333333333 U_In, 0.33112582781456956 U_In, 
0.3377926421404682 U_In, 0.3355481727574751 U_In, 
0.3333333333333333 U_In]

Function: wc_ewc_simplify (expression, definitions...) ¶

Brute-forcing through all combinations of tol[n] in order to find the worst-case combination is O(m^n)-complete and therefore computationally intensive for high numbers of tol[n].

wc_ewc_simplify uses the sign of the derivatives of expression to combine as many tol[n], as possible. The result is an expression that might run much faster through wc_mintypmax and wc_systematic, but that, if the derivate of expression doesn’t change sign in the tol[n] space, still yields the same results for the brute-force approaches to worst-case analysis.

Note that changing the number of tol[n] will change the statistical distribution of the results over the tol[n] space and therefore will change the statistical distribution of the montecarlo method and the results of the root sum square functions.

See also wc_mintypmax and wc_montecarlo.

definitions allows to temporarily asssign values to specific tol[n] during the optimizations (normally optimizagion is done with all tol[n] being zero) which has the side-effect of excempting these tol[n] from the optimization.

Example:

(%i1) load("wrstcse")$

(%i2) vals: [
   R_1= 1000.0*(1+tol[1]*.01),
   R_2= 2000.0*(1+tol[2]*.01)
 ];
(%o2) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_2 = 2000.0 (0.01 tol  + 1)]
                                                          2

(%i3) ratprint:false;
(%o3)                         false

(%i4) assume(U_In>0);
(%o4)                      [U_In > 0]

(%i5) divider: U_Out=U_In*(R_1)/(R_1+R_2);
                                R_1 U_In
(%o5)                   U_Out = ---------
                                R_2 + R_1

(%i6) divider_vals:subst(vals,divider);
                        1000.0 (0.01 tol  + 1) U_In
                                        1
(%o6) U_Out = -----------------------------------------------
              2000.0 (0.01 tol  + 1) + 1000.0 (0.01 tol  + 1)
                              2                        1

(%i7) divider_vals_simplified:lhs(divider_vals)=wc_ewc_simplify(rhs(divider_vals));
                        1000.0 (1 - 0.01 tol ) U_In
                                            2
(%o7) U_Out = -----------------------------------------------
              2000.0 (0.01 tol  + 1) + 1000.0 (1 - 0.01 tol )
                              2                            2

(%i8) wc_systematic(rhs(divider_vals));
(%o8) [0.33333333333333337 U_In, 0.3311036789297659 U_In, 
0.3289036544850498 U_In, 0.3355704697986577 U_In, 
0.3333333333333333 U_In, 0.33112582781456956 U_In, 
0.3377926421404682 U_In, 0.3355481727574751 U_In, 
0.3333333333333333 U_In]

(%i9) wc_systematic(rhs(divider_vals_simplified));
(%o9) [0.3377926421404682 U_In, 0.3333333333333333 U_In, 
                                         0.3289036544850498 U_In]

(%i10) lhs(divider_vals)=wc_mintypmax(rhs(divider_vals));
(%o10) U_Out = [min = 0.3289036544850498 U_In, 
    typ = 0.3333333333333333 U_In, max = 0.3377926421404682 U_In]

(%i11) lhs(divider_vals_simplified)=wc_mintypmax(rhs(divider_vals_simplified));
(%o11) U_Out = [min = 0.3289036544850498 U_In, 
    typ = 0.3333333333333333 U_In, max = 0.3377926421404682 U_In]

Use case for adding definitions (tol["E_Gain"] cannot be optimized without knowing the sign of tol["U_In"]):

(%i1) load("wrstcse")$

(%i2) vals: [
   U_In=1.2*tol["U_In"], /* The input voltage range */
   n_Bits=16,            /* The ADC's number of bits */
   U_Ref=1.2*(1+.01*tol["U_Ref"]), /* The Adc's reference */
   E_Gain=1+1.2e-6*tol["E_Gain"], /* Gain error */
   E_Offset=1.5e-6                /* Offset error */
 ];
(%o2) [U_In = 1.2 tol    , n_Bits = 16, 
                     U_In
U_Ref = 1.2 (0.01 tol      + 1), E_Gain = 1.2e-6 tol       + 1, 
                     U_Ref                          E_Gain
E_Offset = 1.5e-6]

(%i3) ratprint:false;
(%o3)                         false

(%i4) wc_inputvalueranges(vals);
(%o4) 
     [   U_In      min = - 1.2      typ = 0        max = 1.2    ]
     [                                                          ]
     [  n_Bits      min = 16        typ = 16       max = 16     ]
     [                                                          ]
     [  U_Ref      min = 1.188     typ = 1.2      max = 1.212   ]
     [                                                          ]
     [  E_Gain   min = 0.9999988    typ = 1     max = 1.0000012 ]
     [                                                          ]
     [ E_Offset   min = 1.5e-6    typ = 1.5e-6   max = 1.5e-6   ]

(%i5) ndsadc:n_DSADC=((U_In*E_Gain+E_Offset)/U_Ref+.5)*(2^(n_Bits)-1);
                  n_Bits       E_Gain U_In + E_Offset
(%o5) n_DSADC = (2       - 1) (---------------------- + 0.5)
                                       U_Ref

(%i6) lhs(ndsadc)=wc_ewc_simplify(subst(vals,rhs(ndsadc)));
(%o6) n_DSADC = 65535 ((0.8333333333333334
 (1.5e-6 - 1.2 (1.2e-6 tol       + 1) tol     ))
                          E_Gain         U_Ref
/(0.01 tol      + 1) + 0.5)
          U_Ref

(%i7) lhs(ndsadc)=wc_ewc_simplify(subst(vals,rhs(ndsadc)),tol["U_In"]=1);
(%o7) n_DSADC = 65535 ((0.8333333333333334
 (1.2 tol     (1 - 1.2e-6 tol     ) + 1.5e-6))
         U_In                U_Ref
/(0.01 tol      + 1) + 0.5)
          U_Ref

Function: wc_montecarlo (expression, num) ¶

Introduces num random values per parameter into expression and returns a list of the result.

See also wc_systematic.

Example:

(%i1) load("wrstcse")$

(%i2) vals: [
   R_1= 1000.0*(1+tol[1]*.01),
   R_2= 2000.0*(1+tol[2]*.01)
 ];
(%o2) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_2 = 2000.0 (0.01 tol  + 1)]
                                                          2

(%i3) divider: U_Out=U_In*(R_1)/(R_1+R_2);
                                R_1 U_In
(%o3)                   U_Out = ---------
                                R_2 + R_1

(%i4) wc_montecarlo(subst(vals,rhs(divider)),10);
(%o4) [0.3301505377099377 U_In, 0.33276843198354916 U_In, 
0.33406203454153227 U_In, 0.33434833585190965 U_In, 
0.3341006856369802 U_In, 0.3359647531928058 U_In, 
0.32911646313213117 U_In, 0.333158315034511 U_In, 
0.3325173140803672 U_In, 0.3331108406798784 U_In]

Function: wc_mintypmax (expr, [n]) ¶

Prints the minimum, maximum and typical value of expr. If n is positive, n values for each parameter will be tried systematically. If n is negative, -n random values are used instead. If no n is given, wc_defaultvaluespertol is assumed.

See also wc_mintypmax_percent, wc_mintypmax_rss, wc_ewc_simplify and wc_systematic.

Example:

(%i1) load("wrstcse")$
(%i2) ratprint:false$

(%i3) vals: [
   R_1= 1000.0*(1+tol[1]*.01),
   R_2= 1000.0*(1+tol[2]*.01)
 ];
(%o3) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_2 = 1000.0 (0.01 tol  + 1)]
                                                          2

(%i4) assume(U_In>0);
(%o4)                      [U_In > 0]

(%i5) divider:U_Out=U_In*R_1/(R_1+R_2);
                                R_1 U_In
(%o5)                   U_Out = ---------
                                R_2 + R_1

(%i6) lhs(divider)=wc_mintypmax(subst(vals,rhs(divider)));
(%o6) U_Out = [min = 0.495 U_In, typ = 0.5 U_In, 
                                                max = 0.505 U_In]

Function: wc_mintypmax_percent (expr, sigmas) ¶

Like wc_mintypmax, but outputs the tolerance range in percent.

See wc_mintypmax.

Example:

(%i1) load("wrstcse")$
(%i2) ratprint:false$
(%i3) wc_defaultsigma:6$

(%i4) vals: [
   R_1= 1000.0*(1+tol[1]*.01),
   R_2= 1000.0*(1+tol[2]*.01)
 ];
(%o4) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_2 = 1000.0 (0.01 tol  + 1)]
                                                          2

(%i5) assume(U_In>0);
(%o5)                      [U_In > 0]

(%i6) divider:U_Out=U_In*R_1/(R_1+R_2);
                                R_1 U_In
(%o6)                   U_Out = ---------
                                R_2 + R_1

(%i7) lhs(divider)=wc_mintypmax(subst(vals,rhs(divider)));
(%o7) U_Out = [min = 0.495 U_In, typ = 0.5 U_In, 
                                                max = 0.505 U_In]

(%i8) lhs(divider)=wc_mintypmax_percent(subst(vals,rhs(divider)));
(%o8) U_Out = [min = - 1.0000000000000009 %, typ = 0.5 U_In, 
                                      max = 1.0000000000000009 %]

Function: wc_mintypmax_rss (expr, sigmas) ¶

Prints the minimum and maximum of expr, as well as how high the probability is that expr will lie out of that range based on a root sum square calculation and assuming all input ranges will be gauss-shaped.

wc_defaultsigma defines how many sigma of an input value’s tolerance distribution the range of tol[n]=[-1...1] corresponds to.

The RSS methods has a few advantages a brute-force worst-case calculation: It is fast even witput wc_ewc_simplify. It prevents overengineering resulting from assuming all tolerances to add up in a catastrophical way if this only happens in a neglectible number of cases. But it will yield only the correct results if the gaussian distribution of the input data is known.

Due to its nature this method doesn’t support tolerances that aren’t symmetrical. Therefore in that case the tolerances are extended in the direction that is less wide.

See also wc_defaultsigma wc_mintypmax_rss_percent, and wc_mintypmax.

Example:

(%i1) load("wrstcse")$
(%i2) ratprint:false$
(%i3) wc_defaultsigma:6$

(%i4) vals: [
   R_1= 1000.0*(1+tol[1]*.01),
   R_2= 1000.0*(1+tol[2]*.01)
 ];
(%o4) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_2 = 1000.0 (0.01 tol  + 1)]
                                                          2

(%i5) assume(U_In>0);
(%o5)                      [U_In > 0]

(%i6) divider:U_Out=U_In*R_1/(R_1+R_2);
                                R_1 U_In
(%o6)                   U_Out = ---------
                                R_2 + R_1

(%i7) lhs(divider)=wc_mintypmax_rss(subst(vals,rhs(divider)),6);
(%o7) U_Out = [min = 0.49646446609406725 U_In, typ = 0.5 U_In, 
 max = 0.5035355339059328 U_In, Fail = 0.0019731752898266564 ppm]

Function: wc_mintypmax_rss_percent (expr, sigmas) ¶

Like wc_mintypmax_rss, but outputs the tolerance range in percent.

See wc_mintypmax_rss.

Example:

(%i1) load("wrstcse")$
(%i2) ratprint:false$
(%i3) wc_defaultsigma:6$

(%i4) vals: [
   R_1= 1000.0*(1+tol[1]*.01),
   R_2= 1000.0*(1+tol[2]*.01)
 ];
(%o4) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_2 = 1000.0 (0.01 tol  + 1)]
                                                          2

(%i5) assume(U_In>0);
(%o5)                      [U_In > 0]

(%i6) divider:U_Out=U_In*R_1/(R_1+R_2);
                                R_1 U_In
(%o6)                   U_Out = ---------
                                R_2 + R_1

(%i7) lhs(divider)=wc_mintypmax_rss(subst(vals,rhs(divider)),6);
(%o7) U_Out = [min = 0.49646446609406725 U_In, typ = 0.5 U_In, 
 max = 0.5035355339059328 U_In, Fail = 0.0019731752898266564 ppm]

(%i8) lhs(divider)=float(wc_mintypmax_rss_percent(subst(vals,rhs(divider)),6));
(%o8) U_Out = [min = - 0.7071067811865506 %, typ = 0.5 U_In, 
    max = 0.7071067811865506 %, Fail = 0.0019731752898266564 ppm]

Option variable: wc_defaultsigma ¶

Default value: 6

Defines how many sigmas of the gauss distribution that represents the tolerances of a parameter correspond to a tol[n] value of -1...1.

See also wc_mintypmax_rss.

Example:

(%i1) load("wrstcse")$
(%i2) ratprint:false$

(%i3) vals: [
   R_1= 1000.0*(1+tol[1]*.01),
   R_2= 1000.0*(1+tol[2]*.01)
 ];
(%o3) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_2 = 1000.0 (0.01 tol  + 1)]
                                                          2

(%i4) assume(U_In>0);
(%o4)                      [U_In > 0]

(%i5) divider:U_Out=U_In*R_1/(R_1+R_2);
                                R_1 U_In
(%o5)                   U_Out = ---------
                                R_2 + R_1

(%i6) wc_defaultsigma:1$

(%i7) lhs(divider)=wc_mintypmax_rss(subst(vals,rhs(divider)),6);
(%o7) U_Out = [min = 0.4787867965644036 U_In, typ = 0.5 U_In, 
 max = 0.5212132034355964 U_In, Fail = 0.0019731752898266564 ppm]

(%i8) wc_defaultsigma:3$

(%i9) lhs(divider)=wc_mintypmax_rss(subst(vals,rhs(divider)),6);
(%o9) U_Out = [min = 0.49292893218813455 U_In, typ = 0.5 U_In, 
 max = 0.5070710678118655 U_In, Fail = 0.0019731752898266564 ppm]

(%i10) wc_defaultsigma:6$

(%i11) lhs(divider)=wc_mintypmax_rss(subst(vals,rhs(divider)),6);
(%o11) U_Out = [min = 0.49646446609406725 U_In, typ = 0.5 U_In, 
 max = 0.5035355339059328 U_In, Fail = 0.0019731752898266564 ppm]

Option variable: wc_defaultvaluespertol ¶

Default value: 3

Defines how many samples per tol[n] the EWC method of wc_systematic and wc_mintypmax shall use by default.

See also wc_systematic and wc_mintypmax.

Example:

(%i1) load("wrstcse")$
(%i2) ratprint:false$

(%i3) vals: [
   R_1= 100.0*(1+tol[1]*.01),
   R_2= 1000.0*(1+tol[2]*.01)
 ];
(%o3) [R_1 = 100.0 (0.01 tol  + 1), R_2 = 1000.0 (0.01 tol  + 1)]
                            1                             2

(%i4) wc_defaultvaluespertol:2$

(%i5) wc_systematic(vals);
(%o5) [[R_1 = 99.0, R_2 = 990.0], [R_1 = 99.0, R_2 = 1010.0], 
         [R_1 = 101.0, R_2 = 990.0], [R_1 = 101.0, R_2 = 1010.0]]

(%i6) wc_defaultvaluespertol:3$

(%i7) wc_systematic(vals);
(%o7) [[R_1 = 99.0, R_2 = 990.0], [R_1 = 99.0, R_2 = 1000.0], 
[R_1 = 99.0, R_2 = 1010.0], [R_1 = 100.0, R_2 = 990.0], 
[R_1 = 100.0, R_2 = 1000.0], [R_1 = 100.0, R_2 = 1010.0], 
[R_1 = 101.0, R_2 = 990.0], [R_1 = 101.0, R_2 = 1000.0], 
[R_1 = 101.0, R_2 = 1010.0]]

(%i8) wc_defaultvaluespertol:5$

(%i9) wc_systematic(vals);
(%o9) [[R_1 = 99.0, R_2 = 990.0], [R_1 = 99.0, R_2 = 995.0], 
[R_1 = 99.0, R_2 = 1000.0], [R_1 = 99.0, 
R_2 = 1004.9999999999999], [R_1 = 99.0, R_2 = 1010.0], 
[R_1 = 99.5, R_2 = 990.0], [R_1 = 99.5, R_2 = 995.0], 
[R_1 = 99.5, R_2 = 1000.0], [R_1 = 99.5, 
R_2 = 1004.9999999999999], [R_1 = 99.5, R_2 = 1010.0], 
[R_1 = 100.0, R_2 = 990.0], [R_1 = 100.0, R_2 = 995.0], 
[R_1 = 100.0, R_2 = 1000.0], [R_1 = 100.0, 
R_2 = 1004.9999999999999], [R_1 = 100.0, R_2 = 1010.0], 
[R_1 = 100.49999999999999, R_2 = 990.0], 
[R_1 = 100.49999999999999, R_2 = 995.0], 
[R_1 = 100.49999999999999, R_2 = 1000.0], 
[R_1 = 100.49999999999999, R_2 = 1004.9999999999999], 
[R_1 = 100.49999999999999, R_2 = 1010.0], 
[R_1 = 101.0, R_2 = 990.0], [R_1 = 101.0, R_2 = 995.0], 
[R_1 = 101.0, R_2 = 1000.0], [R_1 = 101.0, 
R_2 = 1004.9999999999999], [R_1 = 101.0, R_2 = 1010.0]]

Function: wc_tolappend (list1, list2,...) ¶

Appends lists of parameters from independent sources making sure that tolerances of all elements in one list will stay independent from all elements in the others.

Works like append() in that it appends all values from all of its arguments to make one big list. But this command, if one list happens to contain a tol[n] with the same n as another list, changes one of these n to a new value that makes it independent from all tolerances from the other list.

See also append.

Example:

(%i1) load("wrstcse")$

(%i2) val_a: [
   R_1= 1000.0*(1+tol[1]*.01),
   R_2= 1000.0*(1+tol[2]*.01)
 ];
(%o2) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_2 = 1000.0 (0.01 tol  + 1)]
                                                          2

(%i3) val_b: [
   R_3= 1000.0*(1+tol[1]*.01),
   R_4= 1000.0*(1+tol[4]*.01)
 ];
(%o3) [R_3 = 1000.0 (0.01 tol  + 1), 
                             1
                                    R_4 = 1000.0 (0.01 tol  + 1)]
                                                          4

(%i4) append(val_a,val_b);
(%o4) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
R_2 = 1000.0 (0.01 tol  + 1), R_3 = 1000.0 (0.01 tol  + 1), 
                      2                             1
R_4 = 1000.0 (0.01 tol  + 1)]
                      4

(%i5) wc_tolappend(val_a,val_b);
                            used = 1

(%o5) [R_1 = 1000.0 (0.01 tol  + 1), 
                             1
R_2 = 1000.0 (0.01 tol  + 1), R_3 = 1000.0 (0.01 tol  + 1), 
                      2                             5
R_4 = 1000.0 (0.01 tol  + 1)]
                      4

Function: wc_mintypmax2tol (tolname, minval, typval, maxval) ¶

Generates a parameter that uses the tolerance tolname and tolerates between the given values.

Example:

(%i1) load("wrstcse")$

(%i2) vals: [U_Diode=wc_mintypmax2tol(tol[1],.5,.75,.82),
       R=wc_mintypmax2tol(tol[2],1,1.1,1.3),
       U_In=wc_mintypmax2tol(tol[3],0,0,15)];
(%o2) [U_Diode = 0.034999999999999976 (|tol | + tol )
                                       |   1|      1
 + 0.125 (tol  - |tol |) + 0.75, 
             1   |   1|
R = 0.09999999999999998 (|tol | + tol )
                         |   2|      2
 + 0.050000000000000044 (tol  - |tol |) + 1.1, 
                            2   |   2|
       15 (|tol | + tol )
           |   3|      3
U_In = ------------------]
               2

(%i3) wc_inputvalueranges(vals);
         [ U_Diode  min = 0.5  typ = 0.75  max = 0.82 ]
         [                                            ]
(%o3)    [    R     min = 1.0  typ = 1.1   max = 1.3  ]
         [                                            ]
         [  U_In     min = 0    typ = 0     max = 15  ]

Function: wc_inputvalueassumptions (expr) ¶

Often it is good practice to keep all numeric values with tolerances in a list and to introduce them into the equations only when needed.

wc_inputvalueassumptions in this case can inform the assume database about the range each variable in that list will be in.

See also wc_tolassumptions, wc_inputvalueranges and assume.

Example:

(%i1) load("wrstcse");
(%o1) /home/gunter/src/maxima-code/share/contrib/wrstcse.mac

(%i2) vals:[
    R_1=100*(1+1/100*tol["R1"])*(1+1/100*tol["Temp"]),
    R_2=200*(1+1/100*tol["R2"])*(1+1/100*tol["Temp"])];
                  tol         tol
                     R1          Temp
(%o2) [R_1 = 100 (----- + 1) (------- + 1), 
                   100          100
                                        tol         tol
                                           R2          Temp
                             R_2 = 200 (----- + 1) (------- + 1)]
                                         100          100

(%i3) float(wc_inputvalueassumptions(%));
(%o3) [R_2 >= 196.02, R_2 <= 204.02, R_1 >= 98.01, R_1 <= 102.01]

(%i4) is(R_1>R_2);
(%o4)                         false

(%i5) is(R_1>90);
(%o5)                         true

(%i6) is(R_1>200);
(%o6)                         false

(%i7) is(R_1<200);
(%o7)                         true

(%i8) is(R_1>100);
(%o8)                        unknown

Function: wc_tolassumptions (expr) ¶

Adds the range of the tol[n] contained in expr to the assume database.

See also wc_inputvalueassumptions, wc_inputvalueranges and assume.

Example:

(%i1) load("wrstcse");
(%o1) /home/gunter/src/maxima-code/share/contrib/wrstcse.mac

(%i2) vals:[
    R_1=100*(1+1/100*tol["R1"])*(1+1/100*tol["Temp"]),
    R_2=200*(1+1/100*tol["R2"])*(1+1/100*tol["Temp"])];
                  tol         tol
                     R1          Temp
(%o2) [R_1 = 100 (----- + 1) (------- + 1), 
                   100          100
                                        tol         tol
                                           R2          Temp
                             R_2 = 200 (----- + 1) (------- + 1)]
                                         100          100

(%i3) float(wc_tolassumptions(%));
(%o3) [tol   >= - 1.0, tol   <= 1.0, tol     >= - 1.0, 
          R1              R1            Temp
                    tol     <= 1.0, tol   >= - 1.0, tol   <= 1.0]
                       Temp            R2              R2

(%i4) is(tol[R_1]>tol[R_2]);
(%o4)                        unknown

(%i5) is(tol[R_1]>1);
(%o5)                        unknown

(%i6) is(tol[R_1]<-1);
(%o6)                        unknown

(%i7) is(tol[R_1]<0);
(%o7)                        unknown

(%i8) is(tol[R_2]>2);
(%o8)                        unknown